Prior to the ISU Congress, the notion was circulated that the only reason the Russians were opposed to CoP was that they had not figured out how to manipulate it. The assumption has been that the complexity of the new judging system keeps the judges from knowing where they are placing the skaters, and the trimmed mean eliminates bogus marks. Thus, there is nothing to worry about, and competition will now be a misconduct-free, happy, happy place.
In 1997-98, prior to the introduction of OBO, we did an analysis on how various calculation methods are affected by bias compared to the majority system. That analysis clearly showed that a single trimmed mean (STM) was not effective in defending against bias in simple scoring systems (two marks on 6.0 scale). CoP, however, involves a much more complex computation method, so perhaps STMs might work better under the new judging system. Thus, we investigate here the effect of bias on STMs under the new scoring system.
Assume for the moment you are a "creative" judge who wants to help out your chosen skaters. You could try and keep track of all your marks for the skaters you are interested in, but that is a lot of work. Is there something simpler you could try?
Rather than trying to keep track of anything, why not instead simply mark each element and program component (PC) one step higher or lower than your honest opinion? For each skater you want to help, mark each element one GoE higher than you really think it deserves and mark each program component up an extra 0.25 points. For their nearest rivals mark those skaters down one GoE in each element and 0.25 points in each PC. Then let the chips fall where they may.
Will it work?
Will you get away with it?
Yes.
And yes.
To see why it works, consider the following simple example.
Start with the following group of "honest" marks for one element or PC, where you gave one of the three sixes:
4 5 5 6 6 6 7.
After trimming the high and low marks, your mark counts and the trimmed marks are
5 5 6 6 6,
the average of which is 5.6.
Now increase your honest mark to a 7. The marks are now
4 5 5 6 6 7 7.
After trimming the high and low marks, one of the sevens is eliminated and you have
5 5 6 6 7,
the average of which is 5.8, a net gain of 0.2.
Now increase your mark to a 8. The marks become
4 5 5 6 6 7 8.
After trimming the high and low marks, the trimmed marks again become
5 5 6 6 7,
and the average is still 5.8. Even though your mark is now eliminated, the skater you wanted to help still benefits compared to the honest marks, because the original high score of 7 (which was trimmed for the honest scores) now comes into use. The only way your attempt to help the skater fails is if your original honest marks would have been the highest marks for all elements and program components, or if your honest marks were the lowest marks and remain the lowest marks for all elements and program components.
In this example the skater has been helped by 0.2 points for just one element/PC. In the Men's free skating, for example, there are 19 elements and PCs, so tenths of a point can add up to many points for the skater you want to help.
If you have a "friend" on the panel to work with, the two of you are even more successful.
Suppose the two of you would have given honest marks of 6, but the two of you go crazy and give 8s. The marks become
4 5 5 6 7 8 8.
After trimming the high and low marks they become
5 5 6 7 8,
and the average is now 6.2, a net gain of 0.6, making the two judges three times as effective as a single judge. One of you may become the sacrificial lamb, and have your marks eliminated by the STM (or not, depending on the distribution of marks from the other judges), but the other is guaranteed to slip through no matter how high the two of you decide to mark.
The effect for hindering a skater, by marking them down, should be equally obvious.
To see how well this simple-minded approach to manipulating results works in real competition, we have taken the results from all the 2003 Grand Prix competitions and calculated the effect of judges helping or hindering skaters. Using an interactive program, we have tested various combinations and amounts of bias, for one to three judges working together. The following approach is used in this analysis.
First we calculate the results using the original Grand Prix marks for panels consisting of 3, 5, 7 or 9 judges. We do this calculation for a simple mean computation method and for the CoP single trimmed mean computation method. The results are then calculated again after adjusting the marks from the misbehaving judges for a single skater up one step for each element/PC, and down one step. The process is repeated for all judges and all skaters. The differences between the scores calculated from the unbiased marks and the scores calculated from biased marks are the amounts the skaters are helped or hindered by manipulations of the marks.
The following table is an example of the results for this type of analysis, for all the ladies events in the 2003 Grand Prix. The following tables (short program only, free skating only, and combined event result) show the average point amounts by which a skater is helped or hindered by biased marks from one judge, averaged over all skaters and all judges.
| Judges on Panel | Simple Mean | Single Trimmed Mean | ||||
| Ave Help | Ave Hinder | Total Effect | Ave Help | Ave Hinder | Total Effect | |
| 9 | 0.78 | 0.71 | 1.49 | 0.61 | 0.61 | 1.22 |
| 7 | 1.01 | 0.91 | 1.92 | 0.78 | 0.78 | 1.56 |
| 5 | 1.41 | 1.27 | 2.68 | 1.11 | 0.92 | 2.03 |
| 3 | 2.34 | 2.11 | 4.45 | 1.69 | 1.50 | 3.19 |
| Judges on Panel | Simple Mean | Single Trimmed Mean | ||||
| Ave Help | Ave Hinder | Total Effect | Ave Help | Ave Hinder | Total Effect | |
| 9 | 1.32 | 1.18 | 2.50 | 0.98 | 0.90 | 1.88 |
| 7 | 1.70 | 1.52 | 3.22 | 1.23 | 1.13 | 2.36 |
| 5 | 2.38 | 2.13 | 4.51 | 1.64 | 1.51 | 3.15 |
| 3 | 3.96 | 3.56 | 7.52 | 2.54 | 2.66 | 5.20 |
| Judges on Panel | Simple Mean | Single Trimmed Mean | ||||
| Ave Help | Ave Hinder | Total Effect | Ave Help | Ave Hinder | Total Effect | |
| 9 | 2.10 | 1.89 | 3.99 | 1.59 | 1.51 | 3.10 |
| 7 | 2.71 | 2.43 | 5.14 | 2.01 | 1.91 | 3.92 |
| 5 | 3.79 | 3.40 | 7.19 | 2.75 | 2.43 | 5.18 |
| 3 | 6.30 | 5.67 | 11.97 | 4.23 | 4.16 | 8.39 |
For panels consisting of nine judges (as will be used in ISU competition after the random elimination of three judges from a panel of twelve), one judge on the average can help a skater by 1.59 points and hinder her rival by 1.51 points. Thus, a single judge on the average can erase an honest point difference of 3.1 points between two skaters in a free skating event under the STM computation method and in many cases was found to erase point differences up to 5.8 points. Similar results are obtained for all other events.
As the size of the panel decreases the effect of a single biased judge increases, since the marks from the biased judge makes up a larger fraction of the marks given the smaller number of judges. This has important implications in local competitions where fewer than nine judges are typically used. When the typical five judges are use in a club competition, one judge can skew the point difference between two skaters by over 5 points, and when three are used (as is sometimes the case) the impact is over 8 points!
As an example of two judges working together, the following table shows the effect of two judges on a panel of nine judges helping one skater and hindering her rival.
| Panel of 9 Judges | Simple Mean | Single Trimmed Mean | ||||
| Ave Help | Ave Hinder | Total Effect | Ave Help | Ave Hinder | Total Effect | |
| SP | 1.57 | 1.42 | 2.99 | 1.40 | 1.27 | 2.67 |
| FS | 2.64 | 2.36 | 5.00 | 2.33 | 2.10 | 4.43 |
| Event Total | 4.21 | 3.78 | 7.99 | 3.73 | 3.37 | 7.10 |
When two judges work together we find they will erase an honest point difference of 7.1 points on the average. If three judges help one skater and hinder her rival, it is found that the three judges will erase an honest point difference of 11.4 points on the average.
What effect, then, will these point shifts have on the final places in an event?
To answer that question we need to know the typical point difference between two skaters in events.
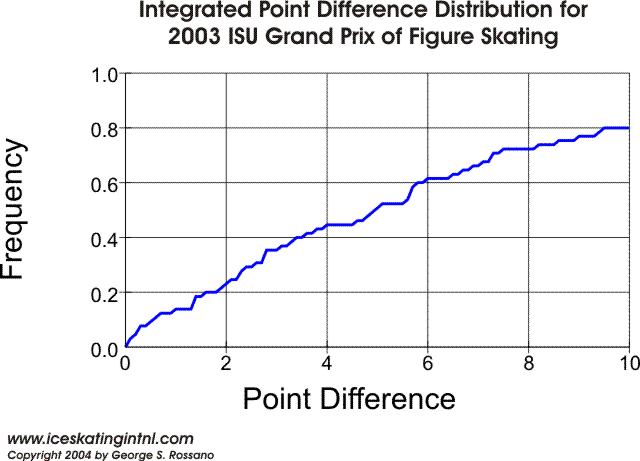
The following graph illustrate the frequency with which sequential places in the Ladies events at the 2003 Grand Prix were separated by some number of points or less (i.e., 1st to 2nd, 2nd to 3rd, 3rd to 4th, etc.).
Read this graph in the following way: Sequential places were separated by 10 points or less for 80% of all cases, sequential places were separated by 4 points or less about 45% of the time, and sequential places were separated by 2 points or less about 24% of the time.

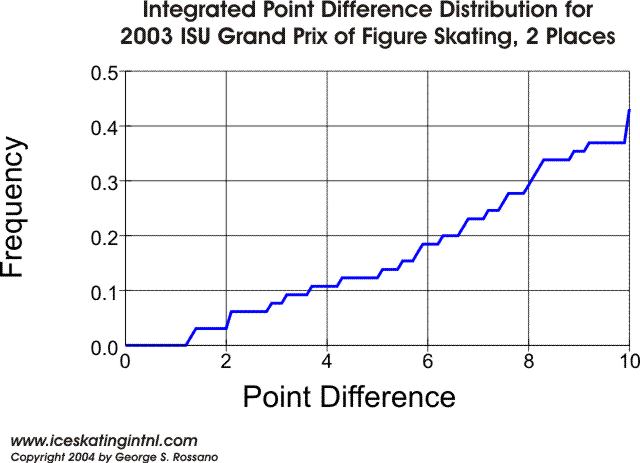
The next graph shows the same thing for skates separated by two places (i.e., 1st to 3rd, 2nd to 4th, 3rd to 5th, etc).
In this case, two sequential places were separated by 10 points or less 43% of the time, two sequential places were separated by 4 points or less about 11% of the time, and two sequential places were separated by 2 points or less about 3% of the time.
Using the simple manipulation method, a single judge on a panel of nine judges can typically erase a point difference of 3 points on the average. Sequential places are typically separated by 3 points or less, 38% of the time; thus, a judge who biases one skater up and one skater down can reverse the places of the two skaters 38% of the time. If random selection of judges is used, there is a 75% chance the judge will not be eliminated in the random draw and biased judges will then be successful about 30% of the time when attempting to manipulate results.
Skaters are also separated by 3 points or less for two places about 8% of the time, so a single biased judge can also move a skater up two places in about 1 attempt in 12.
In comparison, the majority system currently still used in the U.S. (but expected to be replaced next season) allows a single judge to move a skater up or down one place only when the panel is evenly split in the absence of that judge's mark. At the 2003 and 2004 U.S. Nationals, that situation occurred about 4% of the time. Thus, in the majority system, the ability of a single judge to skew the results by one place is significantly less than for the STM method in the new judging system. The ability of a single judge to skew the results by two places in the majority system is negligible (much less than 1%).
When two judges work together on a nine judge panel, they can erase an honest point difference of 7 points. Sequential places are typically separated by 7 points or less more than 63% of the time, and two sequential places (e.g., 1st to 3rd) are separated by 7 points or less 24% of the time. Two judges working together get their way about two-thirds of the time in moving a skater one place, and for one attempt in four can move a skater two places.
When three judges work together on a nine judge panel, they can erase an honest point difference of over 11 points. Sequential places are typically separated by 11 points or less, more than 80% of the time, and two sequential places are separated by 11 points 45% of the time. Three judges get their way more than three-quarters of the time in moving a skater one place, and nearly half the time they will move their skater up two places.
Thus, when two or three judges work together, they can get pretty much any answer they want the majority of the time. There is even the opportunity to move a skater from fourth to first place a small but significant fraction of the time.
The following table summarizes these results for the Ladies events at the 2003 Grand Prix. These results are for panels of nine judges without random selection of judges (the situation we might anticipate for future U.S. Nationals). For panels of twelve judges randomly selected to nine, reduce these values by 25%.
| Number of Biased Judges | Move 1 Place | Move 2 Places |
| 1 | 38% | 8% |
| 2 | 63% | 24% |
| 3 | 81% | 45% |
In club competitions with 3-5 judges, a single judge can erase an honest point difference of 5-8 points, which will skew the results by one place 46-67% of the time. Thus, in a club competition a single judge would get their way about one-half to two-thirds of the time.
If you don't get greedy, no you don't.
In addition to calculating results, the software also calculates "anomaly" statistics for the judges in each event segment. If a judge limits their machinations to just a couple of skaters, then the anomaly statistics do not show a significant change when biased marks are given, even greatly biased marks. In effect, there is such a large variation in the natural spread of the judges' marks that a change of one step in GoE or PCs for a couple of skaters is not statistically significant, since by necessity anomalies must be averaged over all marks and many skaters to be meaningful.
Another way to think of it is that the statistics used to calculate anomalies are closely related to the computation method used to determine the results. If the computation method is unable to filter out the biased marks in calculating the results (which it is), it will also be unable to identify the marks as anomalies and "finger" the misbehaving judge. For example, the point totals in the Ladies free skating in Cup of China had a point difference of 5.28 points in favor of Onda to 46.1 points in favor of Liashenko. With that much spread, a few points up here and down there get lost in the noise.
At Salt Lake a misbehaving judge had to place the Russians first to skew the results, with no place to hide. Because the new scoring system is now point based, a misbehaving judge doesn't necessarily have to score the skater they want to help higher than their rival to be successful. So again, there is nothing difficult to keep track of while judging, just bump up (or down) the scores and see what happens.
For example, suppose in a close event, your honest marks would have Skater-A 10 points ahead of Skater-B in an event segment on your sheet. Your manipulations might result in Skater-A only 2 points ahead of Skater-B for your marks alone; but if all the element and PC marks are split between the two skaters, your help will frequently be enough to allow Skater-B to win. Further, in your defense after the fact you can say, "But my marks had the other skater first. Don't blame me!"
As a second example, suppose the skater you want to help has a five point lead after the Short Program. In the Free Skating segment all one has to do is protect that lead. If your biased marks results in your skater losing the free skating by only 4 points instead of 6 for honest marks, your biased marks have accomplished your goal. The skater you want to win the event may end up losing the Free Skating on every judge's sheet, including yours, but still win the event thanks to your help -- and again you can say after the fact, "How can there be bias, I agreed with everyone else in the Free Skating!"
The greedier a judge gets, the more impact they potentially can have, but their chance of success goes down and their chance of detection goes up slightly (though even if they are caught, it is after the fact and their marks still stand).
For one step in GoE and 0.25 points in PCs, any one judge would have been successful in changing any skater's point total during the 2003 Grand Prix, 95% of the time. Only in a handful of cases did the STM completely prevent this amount of bias from altering the scores. At 0.50 points in each PC the STM was not significantly more successful in filtering bias. Beyond one GoE and 0.50 in PCs, anomaly statistics start to rise and the marks of single judge become more likely to be identified as suspicious.
When two or more judges work together, the natural spread in the marks during the 2003 Grand Prix was sufficiently large that two steps in GoE and 0.50-0.75 in PCs do not look out of place by a statistically significant amount, and provide a huge boost to the skater being helped.
Based on analysis of the actual marks in the 2003 Grand Prix competitions we find the following:
No great mathematical or mental skills are required for a judge to manipulate the results in an event under the new judging system.
Using a single trimmed mean, a single judge, either through misconduct or systematic errors of judgment, will significantly alter the point totals skaters genuinely deserve. These systematic biases will skew event results by 1-2 places for any given skater, a significant fraction of the time. This is due to the fact that the STM computation method has only a limited effect in reducing the effect of bias on point totals, at best reducing bias by only 25% or less compared to a simple mean.
Two or more judges working together on a panel of nine judges, or simply of a like mind, will skew event results a majority of the time.
A single judge on a panel of three or five judges will skew event results by one place a majority of the time.
Under the new computation method and system of evaluating judges, it is impossible to reliably identify the biased judges if they are modest in the manipulation of their marks. Nor can their impact on the scores be mathematically filtered effectively using STMs. It is intrinsic to the computation method and, thus, something the skaters just have to live with.
Copyright 2004 by George S. Rossano